Strategies for Reversing Math Learning Loss

Learning loss can happen due to many circumstances. This article will explore some of the reasons that math learning loss happens and the ways that directors and administrators can implement strategic strategies, systems, and structures to make decisions about instruction that reverses math learning loss. It also provides access to a free printable intervention poster with six steps to building a schoolwide intervention model that identifies, addresses, and reverses math learning loss. 

Math Learning Loss Causes 

Even in a normal school year, learning loss takes place in multiple content areas due to the summer break, extended periods of inclement weather, sickness, the list goes on and on. We saw math learning loss occur due to lack of adequate instructional time during the pandemic school closures. There are many reasons that math learning loss can occur.

Systems and Structures to Stem Math Learning Loss

During my tenure as a district administrator, my team and I worked extremely hard in planning for summer camps, beginning  as early as January to make sure that students entered their next grade level at the same level of proficiency when they exited their previous grade level.

As school or district administrators, you have a very important role to play in your students' success.

Resources, materials, professional development, school schedule, and even the format of a block of instructional time are all things to consider when making decisions year after year.

Let’s explore some systems and structures that can help you with the decisions you will be making in regard to mathematics instruction.

Four-Step Problem Solving Model 

One of the most impactful and beneficial systems you can implement within a grade-level, entire school, or district is a consistent four-step problem solving model. This prevents acronyms from being utilized that can have negative effects on student proficiency during the year and on standardized tests. The concept of a problem-solving model is a simple one:  basically, how your teachers teach students to approach a math problem.

Step 1: Understand the problem

It begins with teaching young learners to understand a problem first. This is not the same as teaching students to locate key words to help them identify whether they need to add, subtract, multiply, or divide. As a matter of fact, that can cause students to get the incorrect answer and the majority of the time, that wrong answer is a choice on a standardized test.

Teach students how to visualize what the problem is asking through role playing, acting, or even drawing. I still use this method today.

Step 2: Apply Strategies

Once a student really understands what the problem is asking, have teachers choose from a variety of strategies to have students choose which ones work for them, as they begin to solve the problem. Some of these strategies include

• Using manipulatives
• CCW (Count, Compute, Write)
• Draw a picture or diagram
• Generalize a pattern
• Guess & Check
• Organize Information
• Simplify the problem
• Use Logical Reasoning
• Work Backwards

Look at the example below and read the dialogue between two students that know what the problem is asking and how they go about using the Guess & Check strategy to figure out the answer. 

Nick and Lauren are working together. They have read the problem and understand that they are to write the numbers so that the equations are true.

Lauren sighs and says, “We’ll never get this. There are too many choices.”

Nick responds, “I agree, but maybe we could try something. Let’s just write the numbers and see what happens.”

Lauren agrees and proceeds to fill in the numbers randomly. As she does so, she says, “Wait, 746 can’t go here; the whole thing is only 342.” She continues, “And it can’t be added to 51 either because it is the biggest number.”

Nick then builds on her thinking, “So it has to go before 489. We are totally getting this.”

By making a guess and checking it, Nick and Lauren came to understand necessary relationships among the numbers they chose and the other numbers in the equation.

Step 3: Justify Your Thinking

The third portion of this problem-solving model can be to have your teachers teach students to communicate and justify their thinking. It is essential that we ask students to communicate their thinking and coincidentally enough, part of our standards. This is achievable regardless of the type of instruction that is taking place: remote, online, in-person, or hybrid.

Here is another example of what this looks like and why it is important to follow-up with questions that force students to justify their thinking.

Philip and Rosa are skiing down a ski trail. 
Philip is 2/6 of the way down the trail. 
Rosa is 2/8 of the way down the trail. 
Who is farther down the trail?

This student is correct; however, how do we know that this student understands fully how to compare fractions? Consider this follow-up question: What if Rosa was 4/8 of the way down the hill?

The student response to the follow-up question is a true testament to their understanding and gives access to new mathematical ideas.

Step 4: Facilitate Discourse

The last component of a problem-solving model can take place at the beginning of every math lesson in your school. Daily Math Activities or Math Warm-Ups are proven to be successful in activating students’ thinking process and making them ready for the lesson ahead. 

Here is a summary of what to think about when planning these activities

• Keep them very brief
• Require collaborative or independent completion
• Encourage students to think like a mathematician
• Have students make connections to themselves, to others, or to content areas
• Clarify student understanding of vocabulary
• Offer repeated opportunities to revisit important mathematical BIG IDEAS

Here is an example of what this activity can look like in a small amount of instructional time.

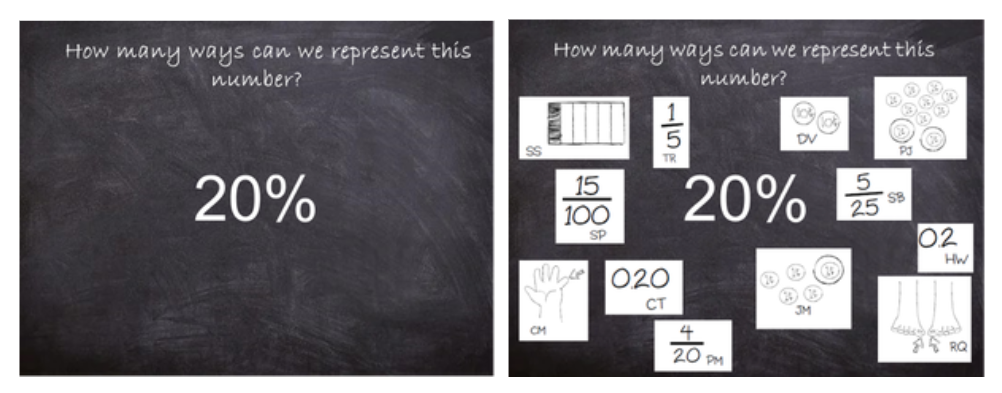
Imagine the conversations that can take place in groups of students or even as a whole group discussion topic. Here are some of the discussion questions that I ask towards the end of this activity in order of the highest amount of teacher support to the lowest amount of teacher support:   

• Look carefully at the chart we created. 
• Are there any representations that you wonder about? 
• Why do you wonder about that representation?
• Why do you think it is important to be able to represent numbers in different ways?
• What math reasoning did you use to determine that your representation is equal to the number on your chart?
• How does understanding whole numbers, fractions, decimals, and percentages help you represent numbers in different ways?
• When would we want to find other representations of a number?

Administrators must make decisions to put structures and systems in place that address math learning loss. Consistent use of the four-step problem solving model outlined in this article will help students better understand problems, apply strategies, justify their thinking, and engage in mathematical discourse. This system combined with your schoolwide efforts to provide intervention will support teachers in meeting the needs of their students.