3 Ways to Improve Your Students’ Problem-Solving Skills

Teaching problem solving doesn’t have to be something you dread. Students can and should enjoy feeling challenged and having to persevere through a difficult task. In this article, we lay out three ways we have found success for incorporating problem-solving into our teaching. Learn more through an on-demand webinar.

Problem-Solving Challenges

Have you ever wondered why students often struggle with problem solving in math? Well, problem solving is… challenging! Additionally, if problem solving is difficult, then teaching how to solve problems is even more demanding. There are some common reasons we believe teachers struggle to support students in developing problem-solving skills. They are:

1. Problem-solving is often taught in conjunction with mnemonics and memorized procedures that are not predictable and that take focus away from the literacy and mathematics of the task
2. Problems chosen are often too routine or familiar for students
3. Problem structures do not vary enough between tasks chosen
4. Instruction seldom includes reflecting and writing about mathematical practices/processes used to problem solve

Even more, word problems...

• have lots of… you guessed it: words! This can be very daunting for all students, especially for linguistic learners who are still mastering the language.
• are structured differently than everyday reading. In literacy, students often learn to think about a paragraph as having a topic sentence, supporting details, and then a concluding sentence. In math, however, word problems start with a lot of details that often don’t make sense until you get to the question (Kelemanik, Lucenta, & Janssen Creighton, 2016).

Improving Student Problem-Solving

Based on our experiences and successes, there are strategic ways incorporating problem- solving into our teaching. Here are three ways that you can support students by incorporating problem solving into your teaching.

Way 1: Use high cognitive demand tasks.

It’s called problem-solving for a reason! There must be an actual problem to solve! After all, a problem isn’t a problem if students already know how to solve it!

Thus, it’s very important to use high cognitive demand tasks in your teaching of problem- solving. These types of tasks engage students in mathematical thinking. They also require students to experience some sort of productive struggle. High cognitive demand tasks may have multiple solutions, or solution paths that are not obvious. They may also have constraints that restrict the number of solutions or strategies.

Teachers’ expectations for student success set the benchmark for students to achieve. When that benchmark is low, student achievement is low. When that benchmark is high, students have an opportunity to rise to that higher level. Providing students with types of tasks that they have not encountered before, and challenging students to make sense of a question, places them at the center of the problem-solving process. Ultimately, then, students are required to think mathematically as opposed to memorizing and regurgitating a set of procedures.

Take a look at the following third grade task:

Norris, K. & Kreisberg, H. (2021). Let's Talk Math. TCM: Huntington Beach, CA.

This task is representative of a high cognitive demand task.
Here’s why:

1. The task has multiple solutions to each question.
2. There are various ways to go about solving the problem.
3. The task is not about applying a memorized procedure such as how to find the area or perimeter of a rectangle, despite the provided labeled wooden board with dimensions.
4. To answer the questions, students are required to use complex thinking as well as a deep understanding of how the concept of fractions connects to geometry

Teaching problem-solving is much more successful when students are provided tasks that require them to think critically.

Way 2: Offer language support, as needed.

Problems can often be wordy and may muddy the water between whether we are assessing reading skills or mathematics. To ensure the focus is on mathematics, we suggest considering which vocabulary words or grammatical structures might present difficulties. This allows teachers to be better prepared to support challenges that students may encounter.

For example, in the Closet Task problem, the word ‘whole’ when read aloud sounds like ‘hole’. The understanding of the word ‘whole’ is vital to the problem—students must comprehend that the whole board represents the denominator, the entire thing. If students are visualizing a wooden board with holes, they will never have the opportunity to show their understanding of the mathematics content.

Therefore, we suggest previewing important vocabulary before students solve a problem in order to ensure understanding of the task at hand. More specifically, we recommend teachers define appropriate Tier 2 and/or Tier 3 vocabulary words, as needed, for the students they serve.

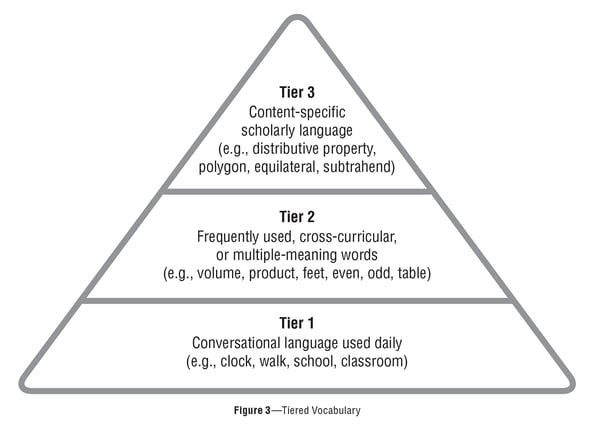
In addition to pre-teaching important vocabulary, we also suggest calling out challenging grammatical structures. These include phrases with modal phrases like “You have to multiply the length by the width to find the area of a rectangle” or conditional phrases such as, “If you multiply any number by zero, then the product will always be zero.”

By supporting students in accessing the language, students may show more success mathematically.

Way 3: Provide opportunities for students to engage in structured discourse.

Problem-solving is often thought of as an isolated topic in math classes. Some might even imagine it to look like students working independently. When presented with a problem in the real world, we often seek others’ help. Problem-solving in math class should mirror the real world. Collaboration is a vital skill that can provide students with the support they need in developing their own abilities to share their thinking and in listening to one another.

In order to collaborate successfully, students need to be explicitly taught how to have a math dialogue. This is why we suggest teachers provide students with specific sentence frames that allow for students to structure their discourse so their conversations are meaningful. Structured discourse also supports students in having equal airtime. Additionally, it ensures that students are listening to understand, not listening to respond.

For example, take a look at this protocol that features structured sentence frames to be used after students have solved a task independently:

Norris, K. & Kreisberg, H. (2021). Let's Talk Math. TCM: Huntington Beach, CA.

Students know exactly how to engage in the conversation. Each student is held accountable for listening and understanding by being asked to rephrase what their partner said. Students then analyze their own strategies and discuss their problem-solving process. Students' learning deepens when they articulate their own understanding as they progress through a meaningful task, as well as when they draw conclusions based on their work.

Problem-solving skills may be enhanced when students are able to communicate effectively about their problem solving process and the mathematical strategies they used.

Successful Problem-Solving

While teaching problem-solving is no easy feat, it doesn’t have to be something to dread! Students can be successful problem solvers when they

1. problem solve using demanding tasks that cause them to critically think
2. collaborate to break down language barriers that often prevent them from accessing the task
3. use structured protocols that promote meaningful mathematical discourse
4. reflect on their problem solving process both orally and in writing

Imagine this:

This scenario illustrates what a classroom can look like where students are active participants in the problem-solving process. In this classroom, students use structured protocols that facilitate them in understanding the task and identifying important information. Students gain self- confidence as they share their thinking and are active listeners in their discussions. They think mathematically, communicate their understandings orally and in writing, and identify connections among mathematical content and strategies.

With the three strategies included in this article, teachers can overcome the challenges of teaching problem-solving and support students in becoming successful, independent problem-solvers. By using high cognitive demand tasks, offering language support, and providing opportunities for students to engage in structured discourse, teachers can empower students to persevere as problem solvers.